Эффективные методы оптимизации процесса производственного планирования
В статье описаны результаты успешного применения метода дискретной оптимизации к решению частной задачи оптимизации производственного планирования, однако характерной для многих производственных предприятий пищевой, химической и фармацевтической отраслей.
Отмечу, что с необходимостью решения подобной задачи часто встречаются и в других отраслях, где в рамках производственного плана значимо время переналадки.
Дана общая структура алгоритма оптимизации решения. Для погружения в тему требуется серьёзное изучение теории графов, теории массового обслуживания и теории расписаний.
Аннотация
В статье описаны результаты успешного применения метода дискретной оптимизации к решению частной задачи оптимизации производственного планирования, однако характерной для многих производственных предприятий пищевой, химической и фармацевтической отраслей.
Отмечу, что с необходимостью решения подобной задачи часто встречаются и в других отраслях, где в рамках производственного плана значимо время переналадки.
Дана общая структура алгоритма оптимизации решения. Для погружения в тему требуется серьёзное изучение теории графов, теории массового обслуживания и теории расписаний.
Постановка задачи
Предположим, что перед нами стоит задача автоматизации производственного планирования на химическом предприятии, которое производит 100 наименований продукции на однотипных производственных линиях. В результате автоматизации мы ожидаем, что процесс планирования будет выполняться без участия человека, а полученный таким образом производственный план не может быть улучшен человеком за приемлемое время.
Подходя к решению задачи оптимизации, нужно прежде всего понять, что именно мы оптимизируем. Иначе говоря, определить целевую функцию, которую мы будем улучшать. В нашем примере мы будем минимизировать суммарное время переналадки. Таким образом нам нужно будет подобрать такую последовательность производственных заказов, при которой суммарное время, которое мы затратим на переналадку будет минимальным.
Для тех, кто незнаком с особенностями организации производства на химических предприятиях, нужно пояснить, что переналадка может занимать существенно большее время, чем само производство конечного продукта (действующего вещества). В процессе переналадки оборудование разбирается, промывается, собирается, проверяется лабораторией на химическую чистоту. А кроме того надо понимать, что матрица переналадок является асимметричной. Т.е. время переналадки от продукта А к продукту В может отличаться от времени переналадки от продукта В к продукту А.
Превратности подходов
Самое частое решение, которое приходит на ум многим неискушенным оптимизаторам - это найти продукты с самым малым временем переналадки и объединить их в пару. Потом присоединить к этой паре следующего ближайшего соседа и действовать так до тех пор, пока мы последовательно не соберем все наши продукты в цепочку. Однако, такой подход лишь гарантирует решение, которое будет лучше самого плохого. На практике, на случайно сгенерированных матрицах переналадок такой алгоритм даст результат, который будет хуже оптимального в 1,5-2 раза.
Давайте попробуем разобраться почему так происходит. Нарисуем 2 точки на плоскости: точку А и точку В. Думаю, все со школы помнят, что кратчайшим расстоянием между такими точками будет прямая (А-В). Теперь давайте нарисуем еще несколько точек на этой прямой (рис.1.1.) Кратчайшим путем между последовательностью точек остается та же прямая из А в В. Если мы уберем первоначальную линию и попробуем последовательно соединить все точки, учитывая только расстояние между ними (рис. 1.1), то очевидно, что полученный результат будет значительно хуже оптимального. Алгоритмы, основанные на средних или медианных расстояниях, также будут показывать результаты далекие от оптимальных.
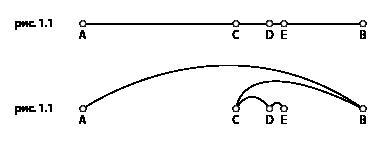
Рис. 1-1.
При поиске решения может возникнуть желание найти все возможные комбинации и выбрать среди них лучшую. Однако на практике такое невозможно по причине того, что число всех возможных комбинаций для 100 продуктов будет равно 9*10^157. Даже если мы решим, что расчет одной такой комбинации будет занимать одну наносекунду, то, я полагаю, что расчет всех возможных комбинаций с использованием всех вычислительных ресурсов, существующих на нашей планете, займет больше времени, чем время существования, самой планеты. Соответственно, такой вариант оптимизации не применим на практике.
Следует признать, что человечество еще не научилось точно решать подобные задачи за “разумное” время, а возможно никогда и не научится. Но что делать, если такие, встречающиеся на практике, задачи все-таки необходимо решать? В этих случаях используются методы дискретной оптимизации, которые хоть и не гарантируют оптимального результата, но позволяют получить решение, которое очень близко к оптимальному.
Использование приближенных алгоритмов. Этапы решения.
На практике решение подобных задач возможно только путем использования приближенных алгоритмов. Суть таких алгоритмов заключается в том, что, зная об экспоненциальном росте сложности такой задачи, мы стремимся строить решение методом проб и ошибок, последовательно его улучшая до тех пор, пока не будет достигнуто максимальное число попыток, либо не будет исчерпан лимит времени.
При решении такой задачи мне проще представлять его как полносвязанный асимметричный ориентированный граф, где вершины являются продуктами, а ребра временем переналадки. Для меня это самый наглядный и логичный подход из всех, с которыми я сталкивался. К сожалению, такой граф редко получается метрическим, что делает невозможным использование части алгоритмов, которые могли бы ускорить процесс поиска решения.
Этап 1.
В первую очередь мы должны выбрать какое-либо начальное решение. Для этого можно просто использовать стохастический комбинаторный выбор
Если хотите прочитать статью полностью и оставить свои комментарии присоединяйтесь к sapland
ЗарегистрироватьсяУ вас уже есть учетная запись?
Войти


Обсуждения 3
3
Комментарий от
Никита Скуратов
| 09 ноября 2016, 11:34
Для меня было честью работать с тобой!
Комментарий от
Александр Дублин
| 14 ноября 2016, 01:38
Никита Скуратов 09 ноября 2016, 11:34
Поздравляю с первой публикацией! Очень познавательно!
Для меня было честью работать с тобой!
Комментарий от
Аркадий Шматов
| 05 мая 2017, 14:11
Не могу тебя найти.
Свяжись со мной, это важно!
arkasheek@gmail.com